[알고리즘] 카운팅 정렬(Counting Sort) - C언어 백준 10989번 메모리 초과 문제 해결!

💻 오늘의 목표 : 카운팅 정렬 완전 정복

 

[버블 정렬, 선택정렬, 삽입정렬]

[알고리즘] 정렬 알고리즘 #1 (정렬 알고리즘 개념, 버블정렬, 선택정렬, 삽입정렬)

 

[퀵 정렬, qsort()]

[알고리즘] 정렬 알고리즘 #2 (퀵 정렬, qsort() 함수)

 

오늘은 정렬 알고리즘 세 번째!

오늘 정리할 정렬 알고리즘은 엄청난 속도를 자랑하는 카운팅 정렬 알고리즘

 

[카운팅 정렬 알고리즘, Counting Sort]

[카운팅 정렬 알고리즘이란?]

• 정렬 알고리즘 중에서 가장 빠른 알고리즘 중 하나
• 원소의 크기가 제한되어 있는 경우에 사용
• 정수나, 정수로 표현할 수 있는 자료에 대해서만 적용 가능
• 입력된 데이터의 크기 범위를 알고 있을 때, 각 데이터가 몇 번 나타났는지 세는 작업을 하여 정렬

[카운팅 정렬 알고리즘 구현 방법]

• 카운트 배열 사용
• 배열의 인덱스를 데이터 값으로 사용
• 카운트 배열의 각 인덱스마다 해당 데이터가 나타난 횟수를 저장
• 카운트 배열 누적합 구함
• 배열을 순회하며 누적합을 이용하여 인덱스값과 인덱스의 값에 해당하는 데이터를 순서대로 출력

 

1. 입력된 배열의 숫자가 각각 몇 번 나오는지 세어 카운트 배열에 인덱스에 따라 저장한다.

 

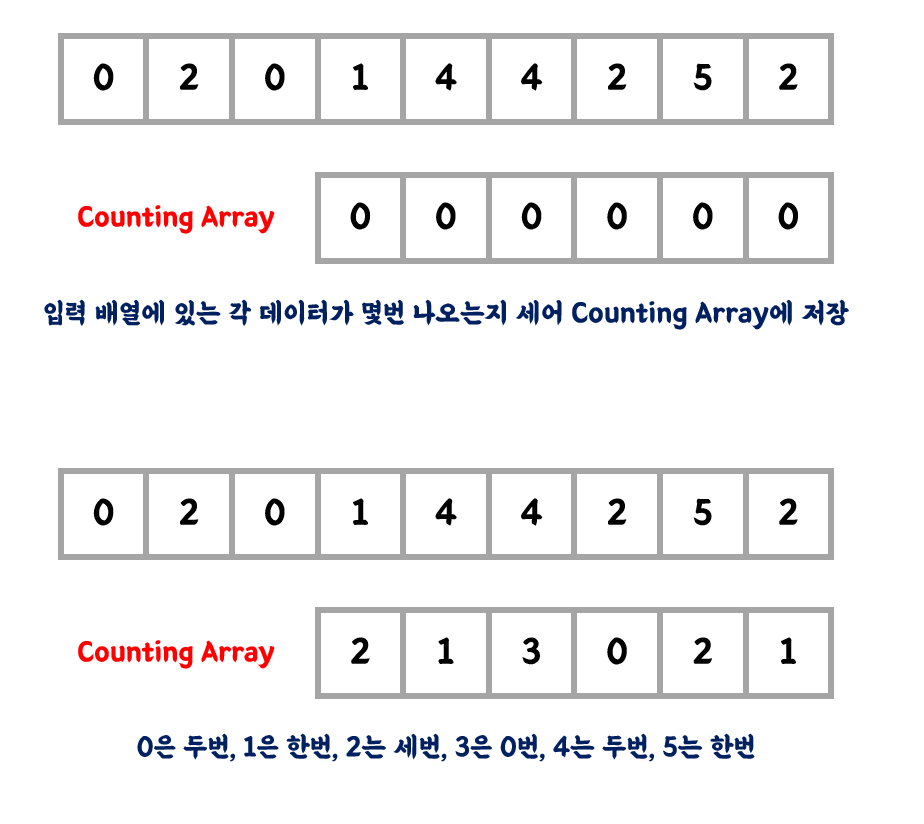
2. 카운트 배열에 있는 데이터를 누적합으로 바꾸어준다.

 

 

3. 입력 배열의 맨 끝 데이터부터 새로 정렬되는 배열에 배치해 주기

 

 

4. 위와 같은 방식을 입력 배열 맨 앞에 있는 데이터에 올 때까지 계속 반복해 주면, 새롭게 정렬된 데이터 배열을 얻을 수 있다.

 

[카운팅 정렬 알고리즘 C언어 구현]

#include <stdlib.h>
#include <stdio.h>

void CountingSort(int inarr[], int n, int outarr[]) {
	int countarr[10] = { 0, };

	for (int i = 0; i < n; i++)
		countarr[inarr[i]]++;

	for (int i = 1; i < 10; i++)
		countarr[i] += countarr[i - 1];

	for (int i = n - 1; i >= 0; i--) {
		outarr[countarr[inarr[i]] - 1] = inarr[i];
		countarr[inarr[i]]--;
	}
}

int main() {
	int arr[10] = { 8, 1, 4, 3, 9, 1, 6, 2, 3, 7 };
	int outarr[10];

	CountingSort(arr, 10, outarr);

	for (int i = 0; i < 10; i++)
		printf("%d ", outarr[i]);

	return 0;
}

 

[카운팅 정렬 알고리즘 시간 복잡도 분석]

카운팅 정렬 알고리즘의 경우 입력 배열의 크기를 N, 입력 배열의 최댓값을 K라고 할 때

• 시간 복잡도 : O(N+K)

위와 같은 시간복잡도를 가지는 이유는 아래와 같다.

1. 각 원소가 나오는 횟수를 계산할 때, 배열을 순회하는데, O(N) 시간이 걸린다
2. 각 원소의 위치를 계산하고, 새로 정렬된 배열을 생성하는데 O(K) 시간이 걸린다.

 

[카운팅 정렬 알고리즘 장단점]

• 장점 : 원소의 크기가 제한된 경우 가장 빠른 알고리즘
• 단점 : 원소의 크기가 큰 경우 메모리 사용량이 커질 수 있음

[카운팅 정렬 알고리즘 문제 - 백준 10989번]

 

10989번: 수 정렬하기 3

 

[문제]

 

 

[첫 번째 시도한 코드]

 

#include <stdlib.h>
#include <stdio.h>

void CountingSort(int inarr[], int n, int outarr[]) {
	int countarr[10000] = { 0, };

	for (int i = 0; i < n; i++)
		countarr[inarr[i]]++;

	for (int i = 1; i < 10000; i++)
		countarr[i] += countarr[i - 1];

	for (int i = n - 1; i >= 0; i--) {
		outarr[countarr[inarr[i]] - 1] = inarr[i];
		countarr[inarr[i]]--;
	}
}

int main() {
	int N;
	scanf("%d", &N);

	int* arr = (int*)malloc(sizeof(int) * N);
	int* outarr = (int*)malloc(sizeof(int) * N);
	for (int i = 0; i < N; i++)
		scanf("%d", &arr[i]);

	CountingSort(arr, N, outarr);

	for (int i = 0; i < N; i++)
		printf("%d\n", outarr[i]);

	return 0;
}

 

맨 처음 코드를 이렇게 짜봤다....

그랬더니 결과는...

 

 

처참하군.... 생각해 보면 입력되는 데이터가 천만 갠데... 이걸 다 저장해 놓고 다시 새로운 배열에 천만 개를 다 저장할 수가... 없을 거라는 생각을 처음엔 하지 못했다. 그리고 고민에 고민을 한 끝에 내린 문제 해결 방법들

 

• 데이터를 받아서 저장을 하지 않고 받자마자 해당하는 인덱스 번호 Counting Arrary에 바로 +1을 해주자!

이렇게 문제를 풀었을 때 생기는 문제는, 데이터들을 오름차순으로 정렬하는 과정에서 어떤 숫자가 어디에 위치해야 하는지 알 수 없다는 점이다. 왜냐? 입력받은 데이터를 저장하지 않았기 때문...

• 저장하지 않은 데이터를 알 수 있는 방법은 없는가?

답은 있다! 바로 Counting Array에서 힌트를 얻을 수 있었다.

 

 

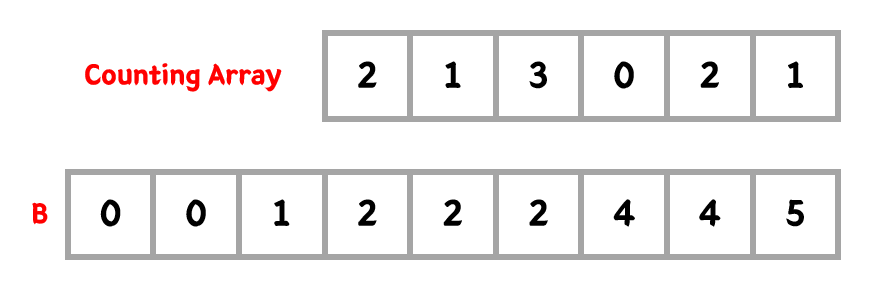
위의 그림에서 아래 있는 Counting Array를 보면 앞에서부터 0 두 개, 1 한 개, 2 세 개, 3 없음....

카운팅 배열 자체가 이미 정렬 개수를 나타내주는 것처럼 보였다...!

 

그래서 코드를 바로 수정해 봤다.

 

[최종 코드]

#include <stdio.h>

void CountingSort(int n) {
	int num, N = 0;
	int countarr[10001] = { 0, };

	for (int i = 0; i < n; i++) {
		scanf("%d", &num);
		countarr[num]++;
	}

	for (int i = 0; i <= 10000; i++) {
		while (countarr[i] != 0) {
			printf("%d\n", i);
			countarr[i]--;
			N++;
		}
		if (N == n)
			break;
	}
}

int main() {
	int N;
	scanf("%d", &N);

	CountingSort(N);

	return 0;
}

결과는....

정답!!!

여기서 드는 의문이 있었다.

• 먼저 제출한 아래쪽에 있는 코드는 누적합 계산을 했던 코드인데, 누적합 계산을 안 한 코드보다 시간이 더 적게 걸렸다.... 누적합 계산으로 시간이 소모될 텐데 왜 누적합을 안 한 코드가 시간이 더 걸릴까...?

---

[최종 정리]

카운팅 정렬은 다른 정렬 알고리즘과 비교해서 입력 배열의 크기가 작고, 원소 크기가 제한되어 있는 경우 가장 효율적이다!

❗❗ 카운팅 정렬 주의할 점

• 입력 배열 크기와 원소 범위가 주어졌을 때, 정렬이 가능한지 확인하기
• 입력 배열이 정렬되어 있는 경우 유용한 배열이다.

---

여기까지 카운팅 알고리즘에 대해 알아봤다.

오늘도 아주 조금 성장한 보보의 코딩일지 끝-!

---

컴퓨터 프로그래밍 전공하는 대학생이 공부했던 내용을 정리하기 위해 적는 소소한 블로그입니다.
잘못된 내용은 댓글에 달아주시면 피드백 감사히 받겠습니다!

[참고한 도서]
- 데이터 구조 원리와 응용
- 이것이 자료구조 + 알고리즘이다
- 프로그래밍 대회에서 배우는 알고리즘 문제해결 전략